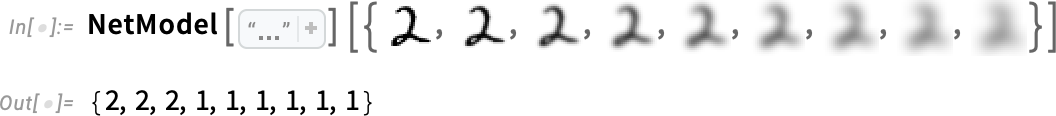What is GPT and Why Does It Work?¶
GPT 的横空出世引起了人类的普遍关注,Stephen Wolfram 的这篇文章深入浅出地讲解了人类语言模型和神经网络的历史进展,深度剖析了 ChatGPT 的底层原理。
讲述 GPT 的能力和局限。
Changelog¶
Latest updated at: 2024-03-01
It’s Just Adding One Word at a Time¶
在 GPT 流利的对话背后,GPT 实际上只专注于做一件事:预测下一个字是什么。
GPT 整个庞大的神经网络,其功能非常简单:根据输入的上下文,预测下一个字是什么。
ChatGPT 的本质就是一个 loop:
for {
next = GPT(content)
if next == EOS {
breal
}
content += next
}
在模型输出结束词(end-of-sequence, EOS)前,不断地循环迭代。
这是黄仁勋对 Ilya 的一次访谈,其中 Ilya 多次强调:最重要的事情,就是预测好下一个词。
LLM 的输出,就是一组词及其对应的概率

不过 GPT 在挑选下一个词时,并不总会挑选概率最高的词,而是会根据 temperature 参数,引入一定的随机性。
一般认为将 temperature 设置为 0.8 会取得不错的输出效果。
词概率从何而来¶
这需要回顾一下 NLP 算法中 n-grams 的历程
首先,选定一个文本数据集,我们就可以计算其中每一个字母的出现概率。
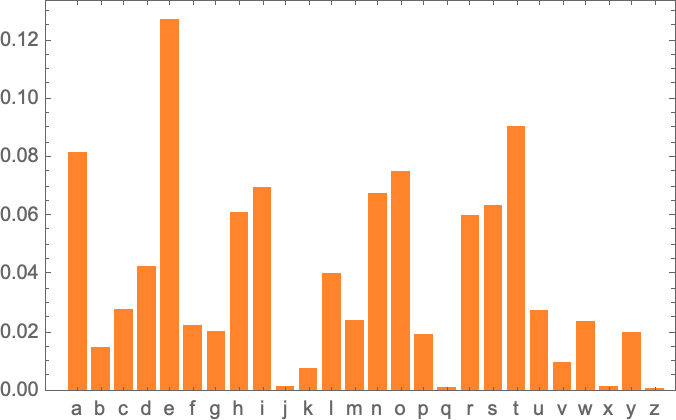
2-grams¶
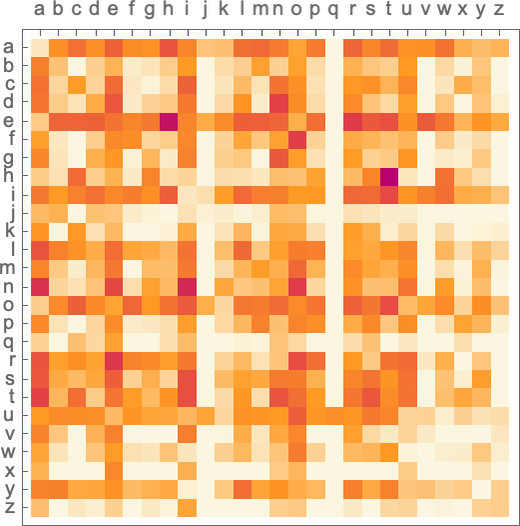
除了计算独立概率,我们还可以计算两个字母的相关概率。
横坐标是第一个字母,纵坐标就对应下一个字母出现的概率。
可以看出,英语单词首字母概率最小的 j、k、q、x、z 都表现为淡色的竖线
基于 n-grams 算法,我们总是根据前 n 个字母,挑选下一个概率最高的字母,就可以实现一个最简单的语言生成模型:

可以看出,随着 n 越大,生成的结果越 make sense
基于词汇的 n-grams 生成算法效果很好,但是它的主要问题是计算量随着 N 的增长而指数级增长。
为 40000 个单词构建 2-grams 会生成 16 亿个组合。3-grams 则有 60 万亿个组合。
该如何计算如此巨量的数据?
最 naive 的办法,就是去每一层扔出铁球,然后测量一下。
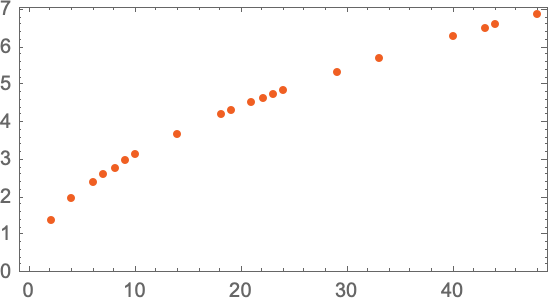
横轴是楼层,纵轴是耗时。
更聪明的做法是,在选定的一些楼层抛出铁球,取得测量值。 然后对这些值进行拟合,构建模型公式。
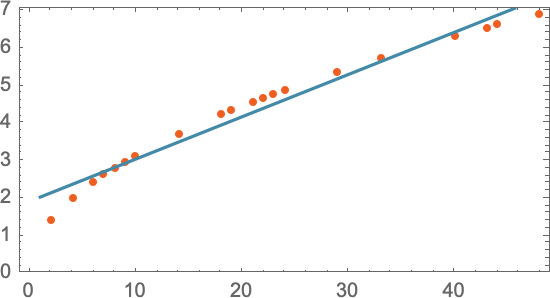
这是一个一元拟合
有时候需要二次方程的拟合,这样我们可以得到一条曲线
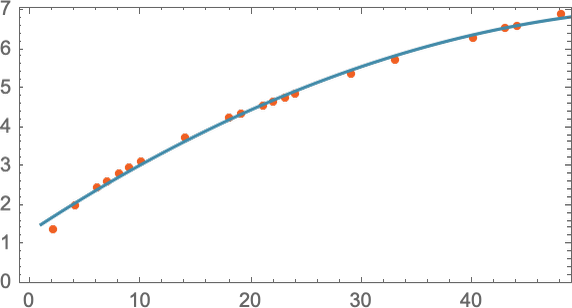
如果情况真的很复杂,那么我们可以继续引入更多的参数。
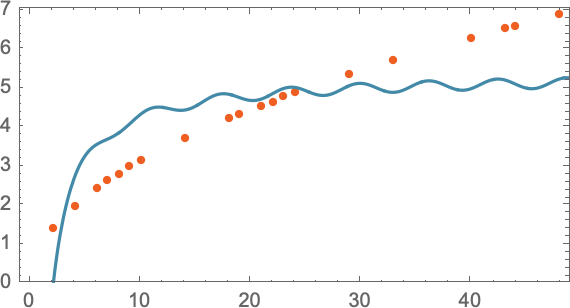
但是参数过多的话,很容易出现过拟合(Overfitting)。
要想模拟人类的语言,大概需要多少参数?
ChatGPT 使用了 1750 亿个参数!实现了类似于 20-grams 的生成效果。
和 n-grams 的天文数字数据量相比,1750 亿还真是个 “小数字” ! 毕竟 3-grams 就需要 60 万亿了。
Models for Human-like Tasks¶
前文提到的扔铁球模型,是可以简化为简单数学运算的模型。
但这个世界上还有很多的问题,难以收敛为简单的数学公式,比如数字识别。
这些在数学上很困难,但是对人而言非常简单的任务,称为 Human-like 任务。
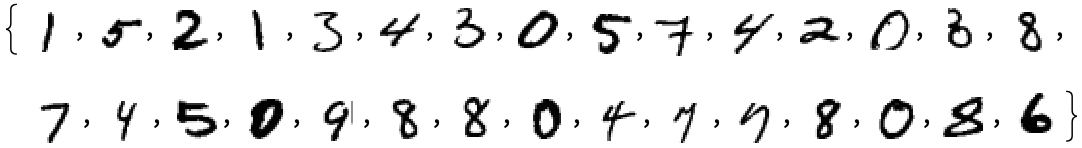
是否能构建一个数学模型,我们只需要把一个图片的全部像素值作为参数输入进去,然后它就能输出这是个什么数字?
事实上确实存在这样的数学模型,它被称为神经网络(neural network),每一次识别需要大约 50 万次计算。
此处暂且把神经网络当成一个神奇的黑盒,后文会对其详细介绍。
可以看到神经网络对于手写数字有着非常好的识别能力
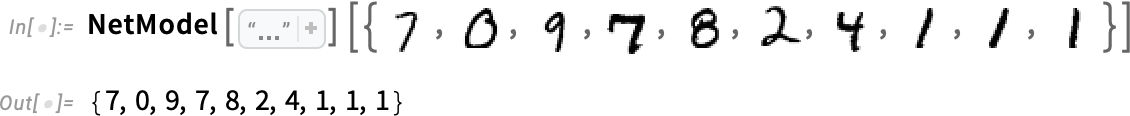
但是神经网络真的错了吗?
你认为它错了,是因为你知道这组数字就是 2。但是神经网络看到的只是单一的图片,如果人类在没有任何上下文的情况下看到这张图片,也能识别出这是 2 吗?
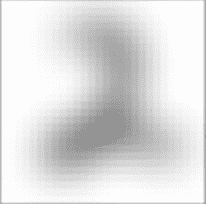
究竟模糊到什么程度,这才是 1 而不是 2?真的存在这样的客观标准吗?
1964 年,美国最高法院大法官波特·斯图尔特(Potter Stewart)在 Jacobellis v. Ohio 案中,对何为淫秽做了如下论断:I know it when I see it。
这一现象,被称为 Polany's Paradox,有些东西,无法用语言表达。 这既是说语言缺乏内生标准,也是说语言无法描述世界的复杂性。
Polanyi’s paradox 对神经网络的挑战就是:人类语言无法表达人类所掌握的知识。而神经网络只能通过人类的语言去学习,那么它能学会人类的知识吗?
Neural Nets¶
正如前面所展示的,目前在认知领域大放异彩的,就是神经网络模型。
这是一种对人脑神经结构的模拟。
人脑中据信有 1000 亿个神经元,每个神经元都通过突触和 1000 个其他神经元相连,神经元每秒可以传递 1000 个电信号。(数字真巧)
通过对脑神经的研究,人类构建了神经元数学模型:
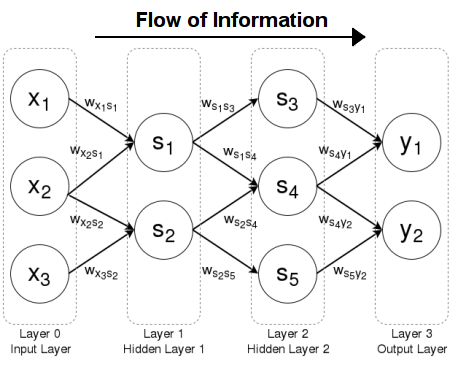
- 基础单元为神经节点和连接,每一个连接都具有不同的权重
- 神经节点和连接构成分层网状结构,信号按照一定的方向在网中传递(绘图习惯从左到右)
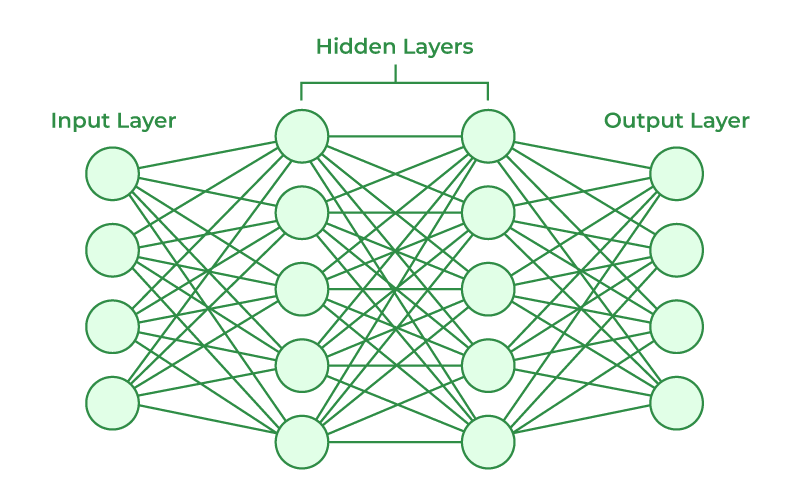
结构非常简单,input layer 接收输入参数,output layer 输出结果。
神经网络也并不是什么经过严肃理论推导的产物。
上个世纪的某一天,某人参照对脑科学的简单理解,随手写了一个试试,发现效果不错,就流传至今。
Attractors¶
神经网络如何实现数字识别?
拿识别 1 和 2 来说,我们希望构筑这样一个空间,这个空间中,所有 2 和 1 的可能写法都聚集在各自的“社群”里。而且这两个聚团间最好存在一个鲜明的分界线。

类推到 10 个数字,这十个数字表现为平面空间中的十个点。
然后我们可以用直线将这十个点进行切分。这些直线和任意两个最近的点间的距离都相等。被直线所包围的区域,也就被归类为中心的点。这个图称为 attractor basins。
所以识别问题被抽象为,在空间中任意一个点,求解距离最近的 attractor point 是哪一个?

Modeling¶
明确了抽象问题后,我们把问题简化一下,再交给神经网络求解。
我们将 attractors 的数量削减为 3 个,然后为其编码(encoding)为 0、-1、+1 三个值。这三个值本身没有任何意义,只是为了方便计算,用不同的整数来进行区分。
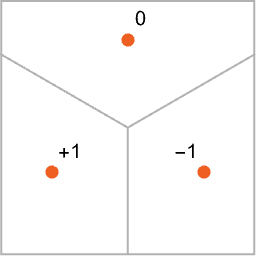
构筑一个简单的神经网络:
- input layer 有两个结点,代表 x、y 坐标
- output layer 有一结点,只输出 0、-1、1 三个值之一
- hidden layer 有两层
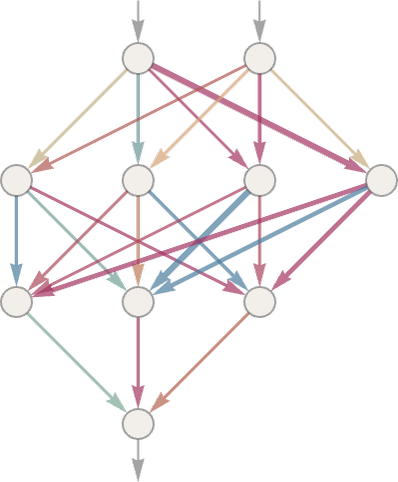
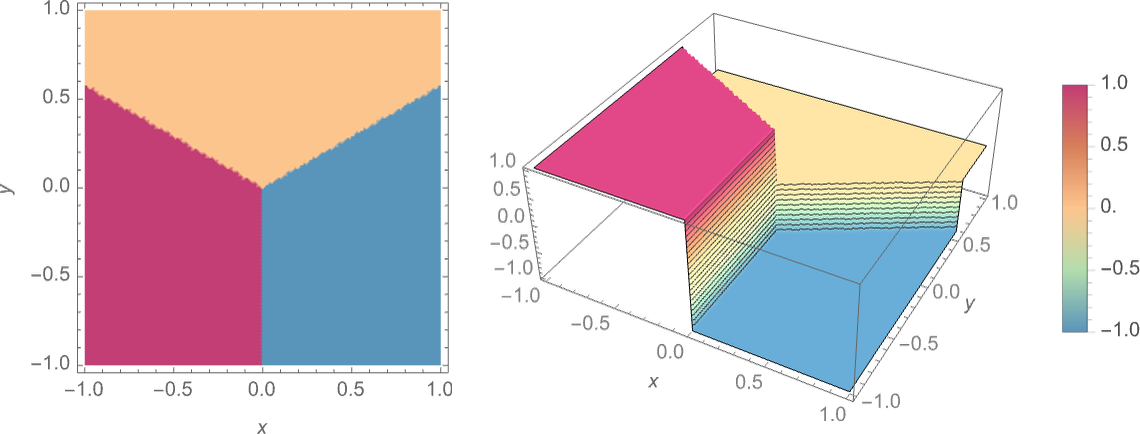
训练数据集的可视化,用三种颜色代表三个 attractors。
可以看到泾渭分明的三个区域,所有的点都根据其所处区域被染成三种颜色。
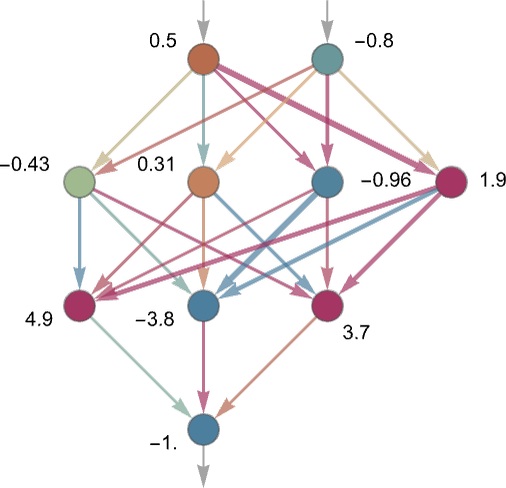
首先在输入层,输入 x、y 坐标。
然后进行神经网络的迭代求值。这其中只涉及加法和乘法。每一个箭头都有一个独立的权重系数(w),假设当前节点的值为 x,那么它就会把 wx 的乘积传递给下一个节点。
下一层的每一个节点都会收到上层 N 个节点传递来的值。按照如下公式计算得到自己的值 value = activation(weightedSum + bias)
bias 是一个随机偏差,activation 称为激活函数。之所以需要这两个东西,是为了给网络引入非线性的不确定性。不然整个网络就成了个线性网络,其表现能力会大幅削弱。

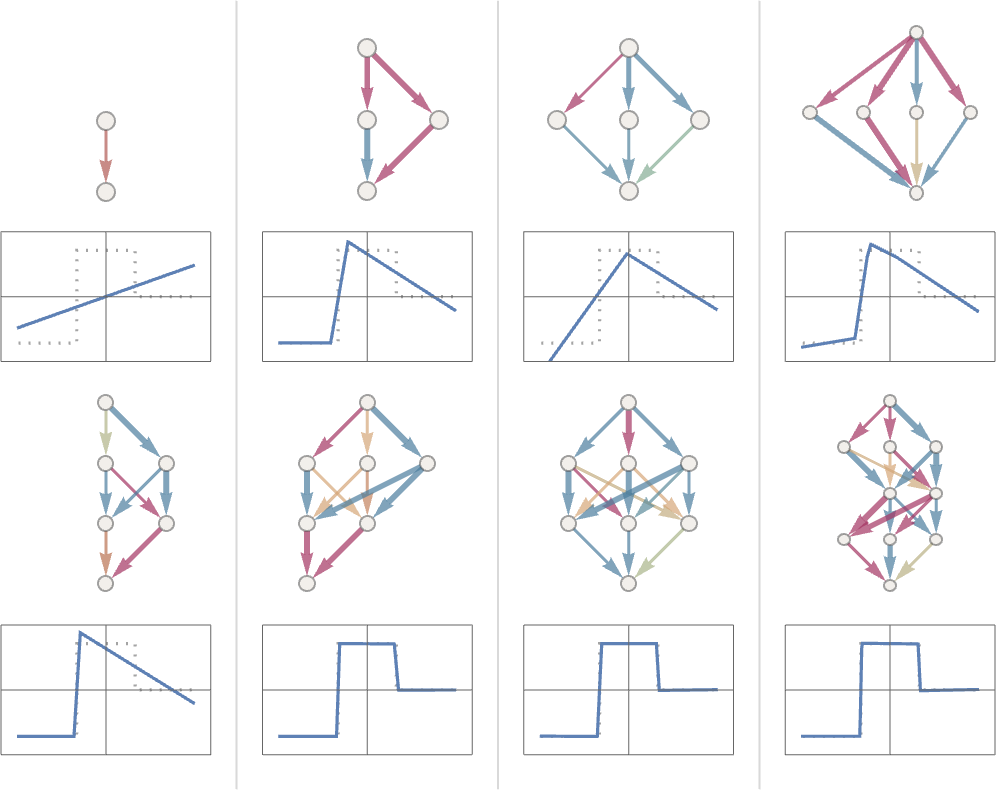
这是一些常用的激活函数。我认为激活函数主要有两个作用:
- 引入非线性变化
- 将节点的值 normalize 到某个固定的取值范围内(一般是 -1~1)
你肯定会想为什么会这样?emm,神经网络这东西很多时候没有为什么,就是某年某日有个人突发奇想这么干了,然后发现跑出来的结果还不错,然后事情就这样了。但是引入非线性变化这个点子还是很直观的,赋予它灵活性,接下来就看它自己了。
到最后,你会发现这些看似高大上的神经网络,实际上只是在反复地做一些加法和乘法。 比如前面那个三层的神经网络,实际上也可以写成下面这个等价的公式:
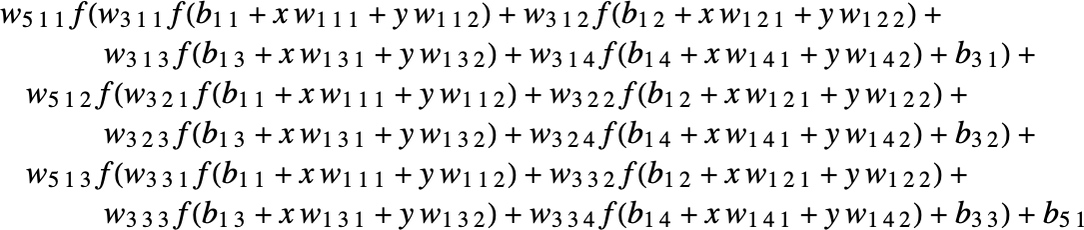
Weights¶
神经网络能力的魔法就蕴含于它的权重和网络结构之中。 严格地说,结构也只是权重的一种表现形式。如果某个连接的权重为 0,那么在结构上就表现为无连接。
我们暂且不管权重是从何而来,可以先尽情地探索一番,比如随意地手动修改权重,看看推理结果会如何变化。
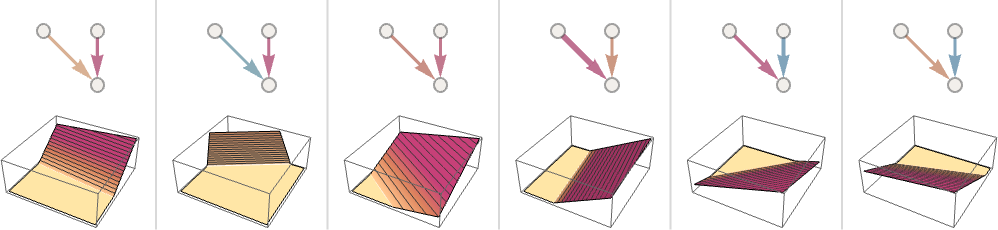
再随意的修改一下结构,看看推理效果变化如何。
可以看出规模越大的神经网络,推理效果越好。虽然边界区域的处理仍然比较混乱,但是正如前文所述,也许根本不存在泾渭分明的区分?
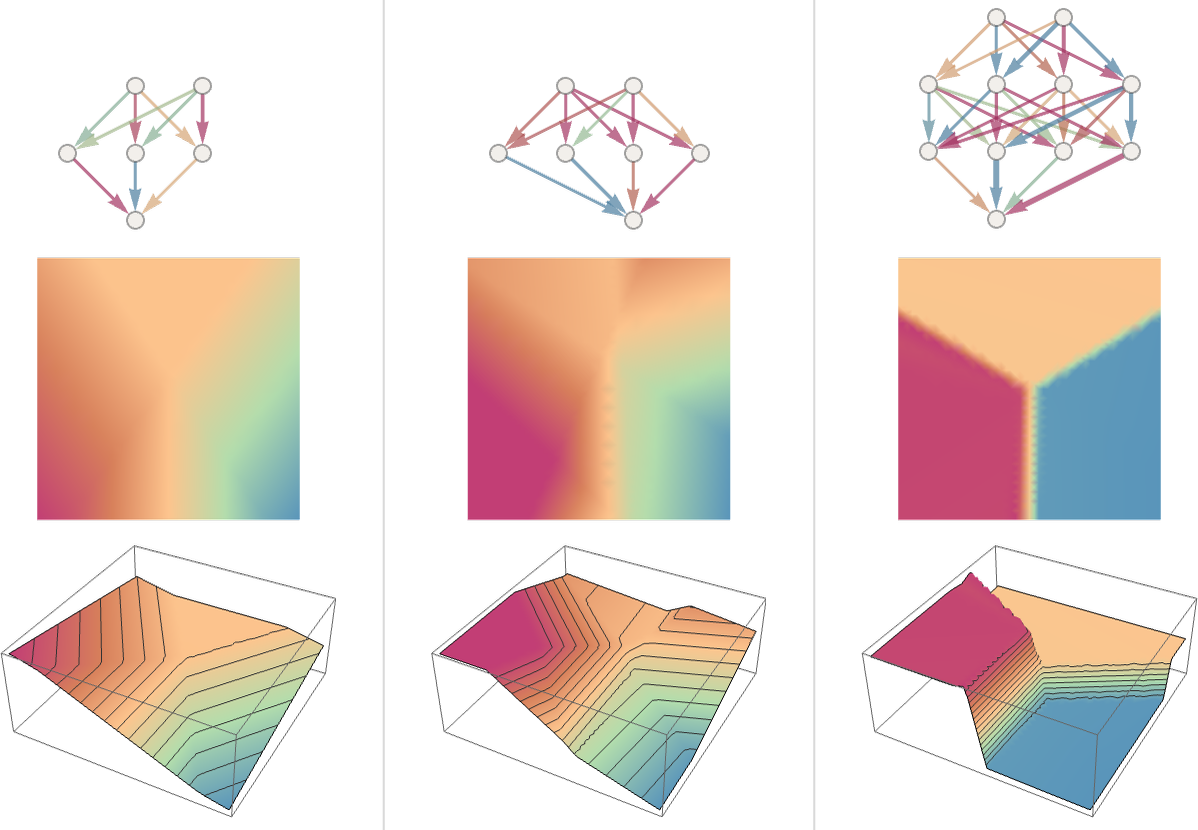
前面的例子只是推理三个点的范围,我们将同样类型的网络扩展到一些更复杂的图片上,也能得到非常好的分类结果。

How¶
神经网络表现出的能力是如此强大,结构又是如此的简单,我们能够从数理原理上解释它究竟是如何做到的吗?
很可惜,不能。神经网络最大的缺点就是不具有可解释性。它很简单,运行也很快,但是我们无从得知它这串数字的背后究竟蕴含着什么理论。
模式识别和区分的背后是人类社群的经验和共识,而神经网络显然从资料集中学会了这个共识,然而我们人类自己都无法清晰地表述这个共识是什么,神经网络当然也不能。
回到一开头时我们曾提到的 Polany's Paradox,有些东西,无法用语言表达。
人类无法精确地认知世界,自然也无从精确地对世界进行形式化描述。最终只能构筑出神经网络这样的黑盒拟合模型。
另一个意义是,人类的知识并不存在 “正确”/“错误” 的严格界线,AI 也无法学习到这个界线,人类的认知是基于经验的,AI 亦如此。
这是一张猫的照片,但是为什么?

Thinking inside neural network¶
前文中,用于识别三个临近点的神经网络有 17 个神经元节点。识别手写数字需要 2190 个,识别猫和狗需要 60650 个。
我们尝试把这 60650 个节点的取值投影到二维平面上,窥探一下神经网络的思维过程。
我们可以轻易地追踪网络中每一个值的变化,还可以随心所欲地将其可视化。
但是,我们仍然难以理解神经网络是如何思考的。
这也是目前 AI 发展的一个困境,我们正在构建一个日益强大的思想机器,而我们对它的思想却一无所知。
Traning¶
终于进入到神经网络科学中最难的部分:训练!
神经网络强大的地方不仅仅在于它可以完成几乎所有的任务,还在于它可以通过样本数据集进行增量训练。
不要怕。虽然最优化理论是非常复杂的数学学科,但是此文中不会出现任何公式,只会提供一些可以凭直觉感受的图像和说明。
你只需要有最简单的数学思维,比如对求极限的概念,即可。
仍然使用简单的例子进行示范,让我们使用如下所示的神经网络,尝试拟合右边的折线。 (输入 x,输出 y)
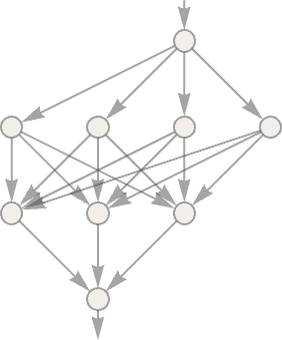 |
 |
训练,指的就是对权重的选择。我们先尝试下随机选择权重,可以看出效果很不好。
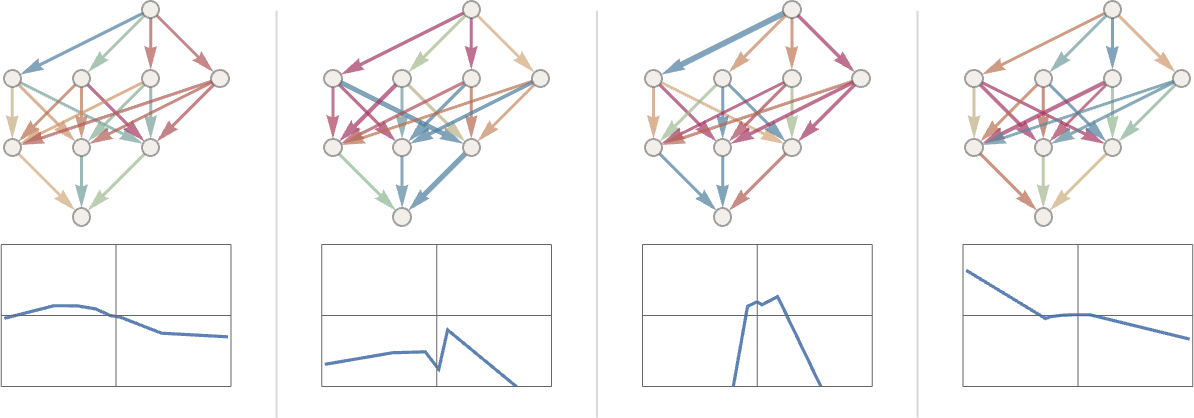
理想情况下,随着数据集的不断输入,神经网络的权重不断调整,输出结果会逐渐趋于完善。
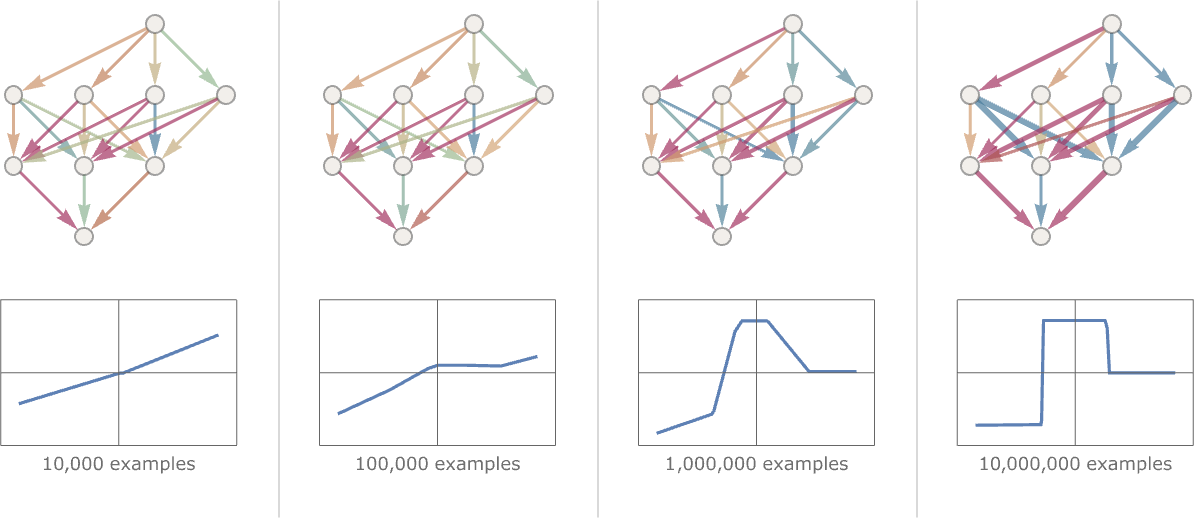
Cost Function¶
所以训练所面临的问题是:改如何调整权重,使得输出结果能逐渐趋近于期望值?
这其实就是数学上很常见的求极限问题,属于微积分的基础知识。
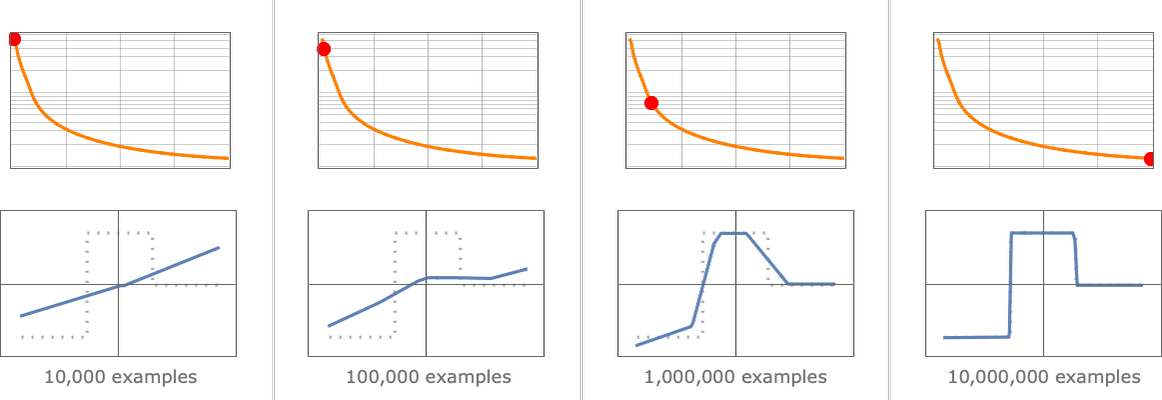
我们可以定义一个损失函数(cost function),这个函数的自变量就是权重值,因变量就是当前输出和期望输出的差值。
于是这成了一个很经典的求极限问题,我们只需要找到这个函数的极小值点,就可以得到最优的权重值。
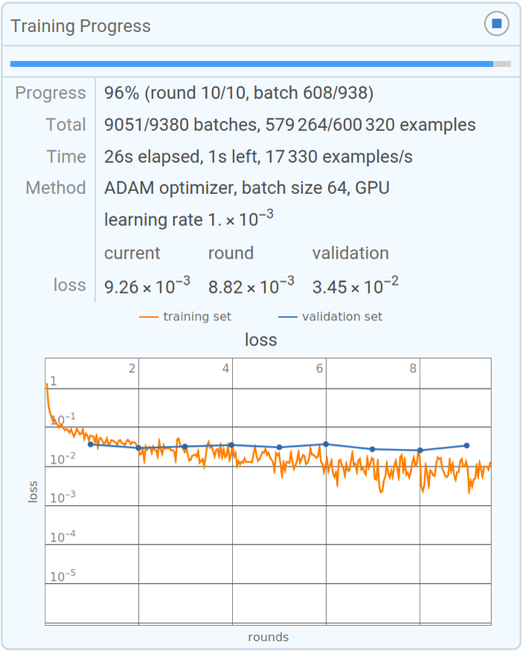
上图是 cost function 的取值变化图,可以看出,随着 cost function 的取值趋近于极小值点,神经网络的拟合效果也越来越好。
为了便于理解,我们继续简化。假设我们正在优化一个仅有两个权重值的神经网络,那么我们可以在一个二维平面上对构造的 cost function 进行可视化。 x、y 轴是权重值,颜色代表 cost function 的取值,据此可以画出一个等高线图。颜色越深,代表计算误差越大。
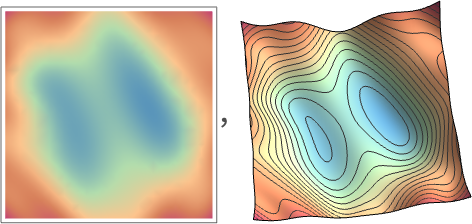
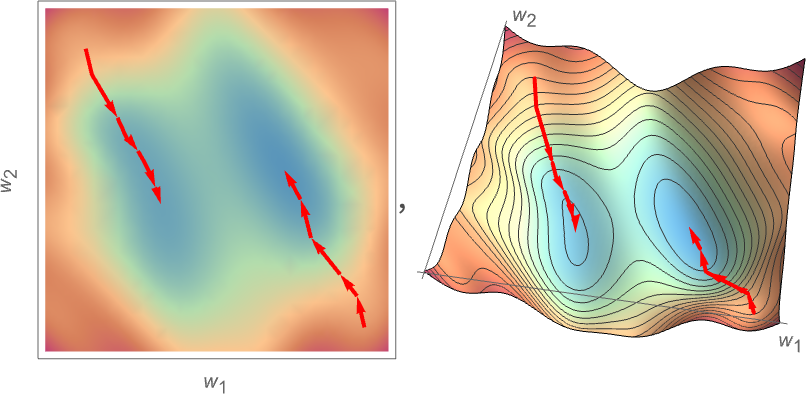
我们把这个等高线图想象成一个山脉,而我们就是一个登山者。在起步的时候随机选择了一个起点,然后我们需要找到一条下山的路径,直到找到这座山脉的最低点。
可惜我们并没有上帝视野,只能看得清周围的山势,所以我们只能从身边的一小步开始,不断地选择向下的方向,直到走到某个盆地的最低点。
这个算法,被很形象地称为梯度下降法(gradient descent)。
Back Propagation¶
面对动辄成千上万的权重参数,我怎么知道下一步该调整哪一个权重,才能让 cost function 的取值更小呢? 这其实就是个很经典的最优化问题,在数值分析领域有大量的工具可以解决这个问题。
从工程的角度来说,最常用的迭代优化方式就是反向传播算法(back propagation)。
Back Propagation 的数学原理其实很简单。
推理是正向传播,就具体的某一次推理来说,根据某组输入,网络计算得出了一个输出,然后这个输出和期望值间存在一个确定的差值。
于是我们从输出节点开始反向回溯,逐一计算每一个上游节点的误差,并且根据每个节点权重公式的导数,计算出每个节点的权重调整值。
这其实就是微积分中很常见的求导问题,只要激活函数是可导的,那么整个网络的误差就可以被很好地传递回去,并且计算好下一步的权重调整值。
神经网络的训练就是不断地重复上述过程,利用大量事先准备好的预训练数据集,每一个训练数据都由输入和期望输出组成。
// 通过随机权重初始化神经网络
neuralNetwork := initWithRandomWeights()
// 遍历训练数据集
for _, data := range trainingData {
// 推理
output := neuralNetwork.inference(data.input)
// 计算误差
cost := costFunction(output, data.expectedOutput)
// 利用误差进行反向传播调整下一轮的权重
neuralNetwork.backPropagation(cost)
}
从前面的等高线图可以看出,梯度下降法虽然简单实用,但是有一个问题是,你可能走着走着就走进了半山腰的一个小凹坑,然后再也走不出来了(因为此时你无论朝什么方向走,都只能走上坡)。
这就是梯度下降法的局部最优解问题,这个问题也没什么特别好的解决办法,最简单粗暴的方式就是多试几次,每次都从不同的随机位置开始。一般来说,你不会运气差到每次都走进同一个小凹坑吧。(这也是为什么有人把训练戏称为炼丹,运气在其中占了很大比重)

训练结果往往会得出不止一个 weights 组合。这意味着我们找到了多个等效的最优解。

但是这些等效模型只是在训练数据集上等效,在更多输入上进行推理时,会产生不一样的结果。 你很难说谁对谁错,每一个模型都是从训练数据集获取了不同的领悟。

这些等效模型某种意义上可以解释天才的存在。
即是是完全一样的网络结构,只是各自有着不同的随机化初始值。 然后接受了一模一样的训练,在校验集上也取得了一模一样的成绩。 但其实每个网络学会的参数都是不一样的。
在更大的范围内进行推理时,这个差距才会显现出来,有些人就是能取得更小的过拟合,在人身上被称为天才的洞察力。
换句话说,一样的天资,一样的后天教育,仍然会随机的诞生天才,这就是神经网络的内在随机性。
Brief History¶
神经网络其实并不是个新东西,它最热门的时候实际上是上世纪 70 年代,当时的研究者们对它寄予了很大的希望,认为它可以解决所有的问题。可是因为算力的制约,神经网络的训练效果并不好,所以它很快就被冷落了。
上个世纪人们也曾大肆鼓吹人工智能,可是随着热潮的退去,人们转而开始采用其他更谦卑的称呼,如神经网络、data mining、machine learning 等。
突破性的发展来自 2012 年 AlexNet 的横空出世,借助 NVIDIA GPU 和一些设计创新,AlexNet 再度提出了那个如今已人尽皆知的道理: “神经网络的能力和其复杂度息息相关!” 这一概念,后来被称为 deep learning。
AlexNet 的作者为 Alex Krizhevsky、Geoffrey Hinton 和 Ilya Sutskever。后两位的名字如今已是如雷贯耳。
The Practice and Lore of Neural Net Training¶
本章介绍神经网络训练过程中的一些实践经验和传说。
神经网络的训练更像是艺术而不是科学,人们在不可解释的混沌中摸索和检验。
很多成果都没有相应的理论支撑,只是无数的试验者们通过实践发现有效。
Human-Like Process¶
过去人们曾经试图为不同的任务设计不同结构的神经网络,但后来发现,神经网络在不同类型的任务上表现出了很好的泛化能力。
简而言之,你不需要为不同的任务去设计不同类型的网络。网络几乎是万能的,其能力只和复杂度有关系。
Wolfram 认为,这是因为我们试图让神经网络解决的都是 human-like process,所以它才表现出如此显著的泛化能力。
Misunderstanding: make the neural net do as little as possible¶
早期,人们试图对神经网络的功能进行解构,按照最小功能集去训练小的单一功能的网络。然后再将这一系列网络组织起来。
但是后来发现,最好的训练方式是 end-to-end,直接用输入和输出去训练大网络,由神经网络自发形成功能层。
Misunderstanding: implement functional component¶
另一个尝试是在神经网络中引入预设的功能单元,扮演类似硬件加速的角色。但是目前看来效果仍然不如直接训练简单网络。
不过这些失败的尝试并不意味着人们没有对数据进行结构化的处理,也取得了如 RNN 或 transformer attention heads 这样的结构化成果。
当神经网络复杂度达到一定的阈值后,推理效果就不会再上升。 一个裁剪思路是,如果所有的数据都流经部分结点,那么其他结点就可以被裁剪掉。
没有中间层的神经网络称为 感知器(perceptron),只能模拟线性方程。 有一个中间层的网络就可以拟合任意函数,只要有足够多的结点。
给数据打标记需要巨大的人工成本,更多的时候是想办法去找现成的标记数据。
比如通过影视多语言字幕可以获取到翻译数据集。通过图片的 alt 标签可以获得多模态的训练数据。
比起从零开始训练,直接利用已有模型进行迁移学习(transfer learning),也可以节省大量数据和时间。
迁移学习中还有一个窍门是反复重复使用同一个数据集,这也许就和人类的反复背诵类似。
训练耗时和数据量、模型大小有关系,但是具体耗时多少很难定量计算。
尽管在 cost function 最优化中使用了微积分方程,但是事实表明计算精度并不重要,大部分时候 8bits 的精度就足够了。
现有的训练方式从自然界的角度来看是很愚蠢的,在 GPU 上执行大量线性计算。 没有理由在未来不会出现某种真正意义上的并行优化算法,就像大自然每天做的那样。
(也许忆阻器能做到?)
a Network Big Enough Can Do Anything?¶
像 ChatGPT 这样的东西的功能似乎是如此令人印象深刻,以至于一个人可能会想象, 如果能够“不断进行”并训练更大更复杂的神经网络,那么它们最终将能够“做任何事情”?
如果你想解决的问题都属于人类的直觉思维,那么神经网络也许确实可以。
但是这类问题的本质在于背后存在一个浅显的抽象模式,但是世界上的问题并不都是可以被简化的。 如非平凡数学(Nontrivial mathematics)这类的问题,统称为 irreducible computation 问题, 这些问题除了遍历计算外没有任何简化办法。(也就是俗称的 NP 问题)
大脑所擅长做的事情,就是从经验中提取模式,从而简化问题,然后在日后的情境中利用习得的模式快速解决问题。
大脑几乎无法不借助外力解决 irreducible computation,比如求解素数、旅行家问题等等。
直到人类发明了图灵机,图灵机可以高效地求解计算问题。
Irreducible Computation¶
computational irreducibility 使得意外总是会发生。
NP 问题无法简化,而人脑/神经网络只能学会简化的拟合模型,所以永远无法消除误差。
一个非常经典的例子就是人类的科学发展。 宇宙是 NP 复杂的,人类的科学进程就是试图用一个个的简化模型去拟合这个世界,直到随着工程进步探索到新的领域(新的数据集)后遭遇误差,然后继续进行下一轮的训练。
当然,就像人类依赖计算机一样,你可以在神经网络中通过 tools 为其提供计算能力,比如 function callings。
但是这些 tools 对于神经网络而言是完全的黑盒,神经网络无法了解其中的计算细节。
所以计算能力(computational capabilities)和可训练度(trainable)存在根本性的矛盾。 你引入越多的 computational tools,可训练度就会越低;反之,你的神经网络越纯粹,计算能力就越差。
目前的神经网络实际上比人脑更糟,它的推理在神经网络中的流动是单向的, 推理步骤由层数所限定,也就是说它无法完成任何超过它层数的推理步骤。计算能力和图灵机完全无法比拟。
The Path Integral Formulation¶
稍微在理论的边界走远一点点。
你能想象世界上实际上根本不存在任何因果律吗?你能想象这个世界上实际上任何可能发生的事情都会发生吗,并且还能够在宏观世界留下它们的痕迹。
欢迎来到费曼的神奇世界,推荐阅读《QED:光和物质的奇妙理论》。
谈到这一点是希望大家对世界的复杂度有一个感性的认知。宇宙的每一件事情都是并行遍历的。
世界是如此复杂,实际上人类无法准确地描述或计算任何最简单的现象。
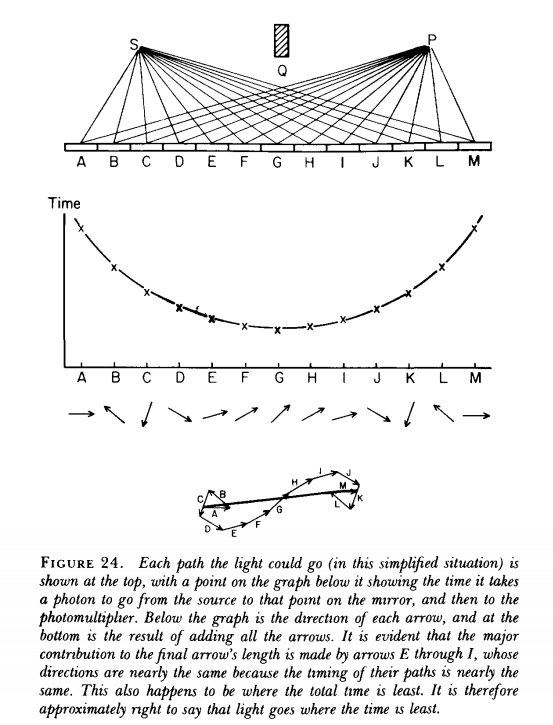
拿最简单的镜面反射来说,中学物理告诉你反射点只是镜面的一点,但其实这个世界从任何一个可能的路径都进行了概率求和。
你可以在非反射点的地方挖掉一些看上去根本没有被光照到的镜面,来改变反射光的强度。
无论是量子世界的叠加态,还是费曼的路径积分,似乎都预示了这么一个世界:
一切可能发生的事情都会发生,结果赋予过程以意义,事件概率不是发生的概率,而是其显现的概率。
并不存在可能性和必然性的区别,所有的事情都是必然的,所有可能发生的事情都发生了。
所以观察者对于世界是无关紧要的,观察者只是让世界以观察者的方式现形。
The Collapse of Human Mythology¶
回到 GPT 的话题来。过去这次 GPT 令人惊叹的表现,让很多人以为计算机世界迎来了革命性的进步。
但实际上不是的,计算机的能力并没有特别大的变化,反而是,其实是人类的能力出现了“巨大降级”。
GPT 证明了写文章实际上不是 irreducible computation 问题,而是 computationally shallower(浅计算)问题。
也就是说,如果有朝一日我们可以制作一个超大规模的神经网络,那么确实可能构建一个 AGI,它也许能够完成人类大脑能做的任何事情。
但是,这也就是它的极限了。它对于自然世界(的 NP 复杂本质)仍然一无所知。
它会无限的接近于人类,但是和我们所使用的自然工具,如计算机,仍然存在着本质的不同
The Concept of Embeddings¶
Embeddings 这个词在 LLM 领域频繁出现,此前分享过的 LLM RAG Technology Overview 中的 RAG 也是高度依赖于 embeddings 所生成的词向量。
本章就会详细介绍 embeddings 究竟是什么。
神经网络基于数字,所以在推理文字时,需要先将文字转换为数字
embeddings 是一种映射方法,可以将文字转换为一个向量。这个向量是当前模型的 meaning space 空间内的一个坐标。
这个 meaning space 来自于神经网络对训练数据集的理解,如果两个词在语料库中表现为同义词,其坐标也应该非常接近。

有点抽象?没关系,我们先回过头看看神经网络的推理流程。
神经网络的最后一层,被称为 softmax 层,负责按照预设的结果集,输出每一个可能结果的概率。
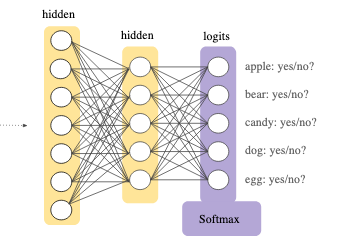
而在 softmax 的前一层网络,就是一组包含着一大堆数字的数组,这一层的取值,其实就是 embeddings 的值。
比如我们之前识别手写数字的神经网络中,4 的 embeddings 结果就是:
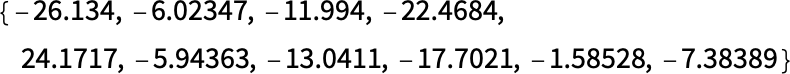
有趣的是,不同的手写体具有不同的 embeddings 值,而全部会被 softmax 识别为同一个数字。
说明 embeddings 值内存在一些模式本质的信息,虽然目前我们还不知道它是什么。

这种基于 embeddings 在 meaning space 里寻找近似关系的行为,和人类思维非常相似,适合解决基于认知的判定问题。
我们再介绍一些关于语言处理的基础知识,下一章就要揭开 GPT 背后 transformer attention 的神秘面纱了。
为了将语言输入到神经网络,需要想办法将其转换为数字。
最简单的做法就是枚举所有的常见词,然后将其映射为递增的整数。这一流程在 NLP 中称为 label encoding。
在 GPT-2 中,就是枚举了 50000 个常见词,如 the -> 914、cat -> 3542。
Inside ChatGPT¶
终于要开始介绍 GPT 内部的工作原理了!
前文讨论的全连通神经网络,每一层的每个结点都和前后层的每个结点互相连通。 这种网络虽然强大,但是计算成本非常高,如果数据集存在明显的结构,是可以据此简化网络结构的。
早期处理图片时常用 CNN(Convolutional Neural Nets) 网络,图片上的每个像素点只会和附近的像素点相连接。
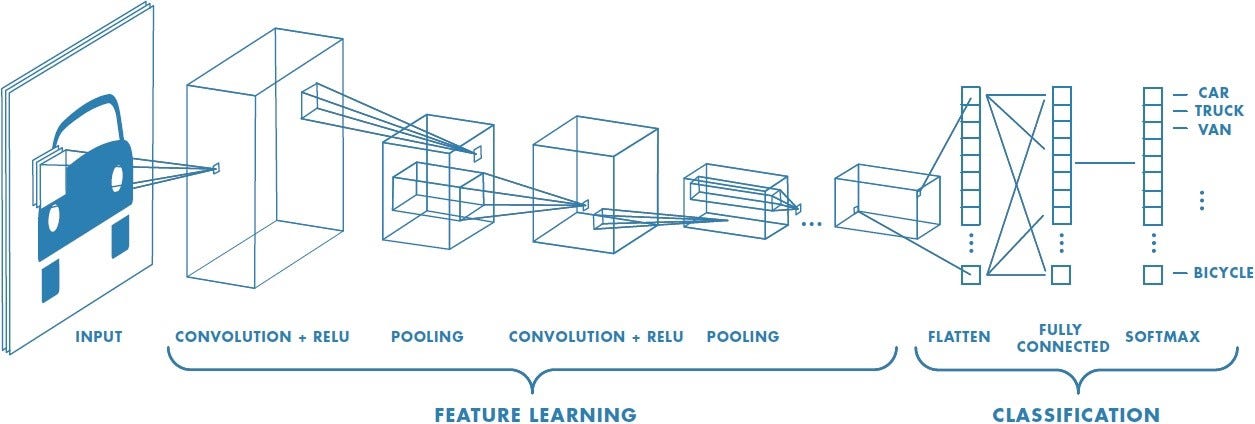
Brief History¶
- 1943 年提出人工神经网络;
- 2014 年发表深度学习(AlexNet);
- 2015 年 Bahdanau 提出 Attention 机制优化 RNN;
- 2015 年 OpenAI 成立;
- 2017 年 Google 发表 Transformer,提出不需要 RNN,只要 Attention 就够了;
- 2017 年 OpenAI 发布基于 transformer 的 gpt-1;
- 2019 年 gpt-2;2020 gpt-3;2022 ChatGPT
可以看出,自从深度学习被提出和广泛应用以来,神经网络的发展就进入了快车道。
RNN¶
传统神经网络是单向推理,一次输入,一次输出。
RNN 是多轮迭代,计算网络称为 RNN Cell,每次读取输入的一部分(如一个词),推理后得出 output 的一部分和一个中间结果(hidden state)。然后进入下一轮迭代,hidden state 会和 input 融合后作为后续的输入。不断重复这一过程直到全部推理结束。
(某种意义上,这个 hidden state 有点像 n-grams)
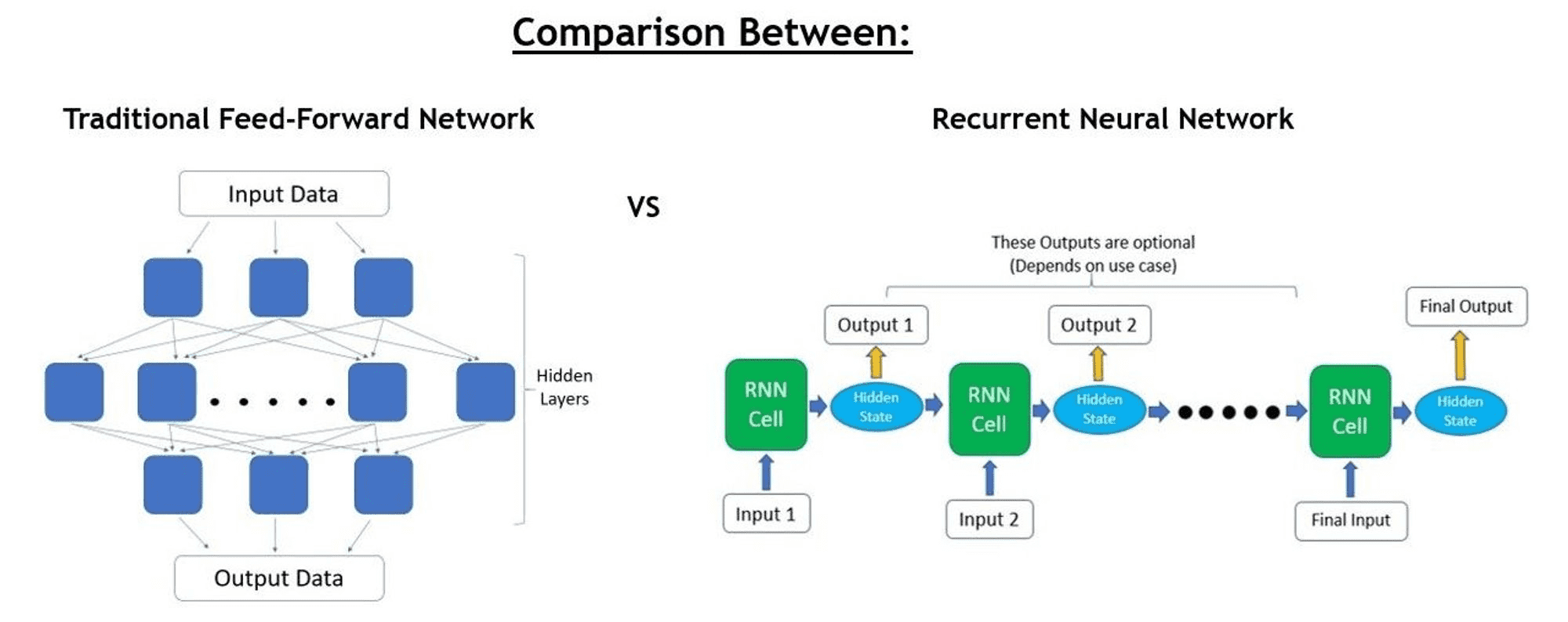
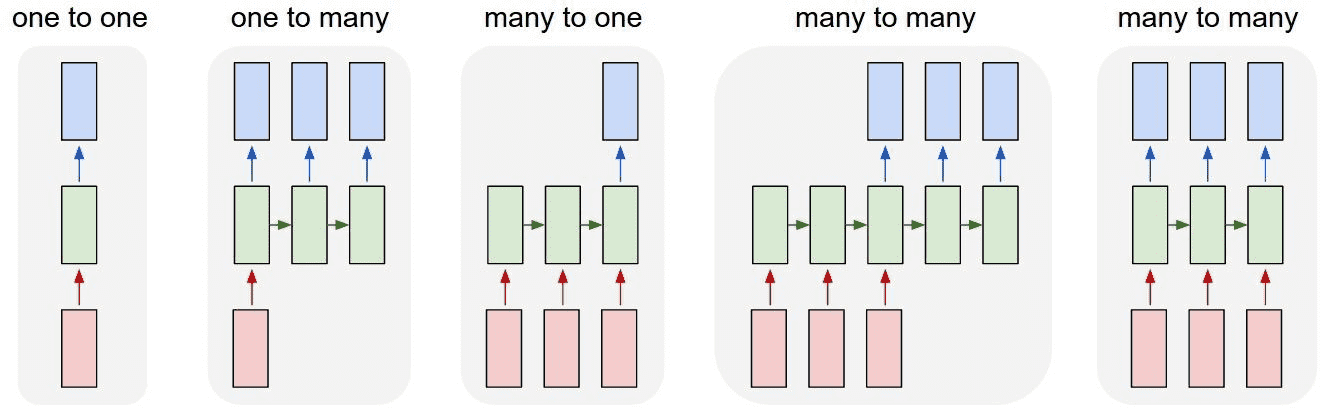
RNN 的 Cell 设计使其输入、输出的长度具有很大的灵活性,可以像普通网络一样单次输入单次输出,也可以多次输入多次输出。而 hidden state 的设计使得每一次输出都可以学习到之前的上下文信息,使其非常适合处理序列问题(sequential problems),如文本翻译。
RNN 的结构也在不断迭代,比如最常见的 seq2seq(专职处理输入的 encoder & 专职处理输出的 decoder)结构,此处略去。
Attention Mechanism¶
RNN 的缺点是,每一轮的输出,只接收了上一轮的 hidden state,当输入比较长时,RNN Cell 可能会遗忘更早的上下文信息。简而言之,RNN 负责输出的 decoder 缺乏全文上下文意识,而更关注于邻近的前几个词。
2015 年德国科学家 Bahdanau 提出了注意力机制(Attention)。
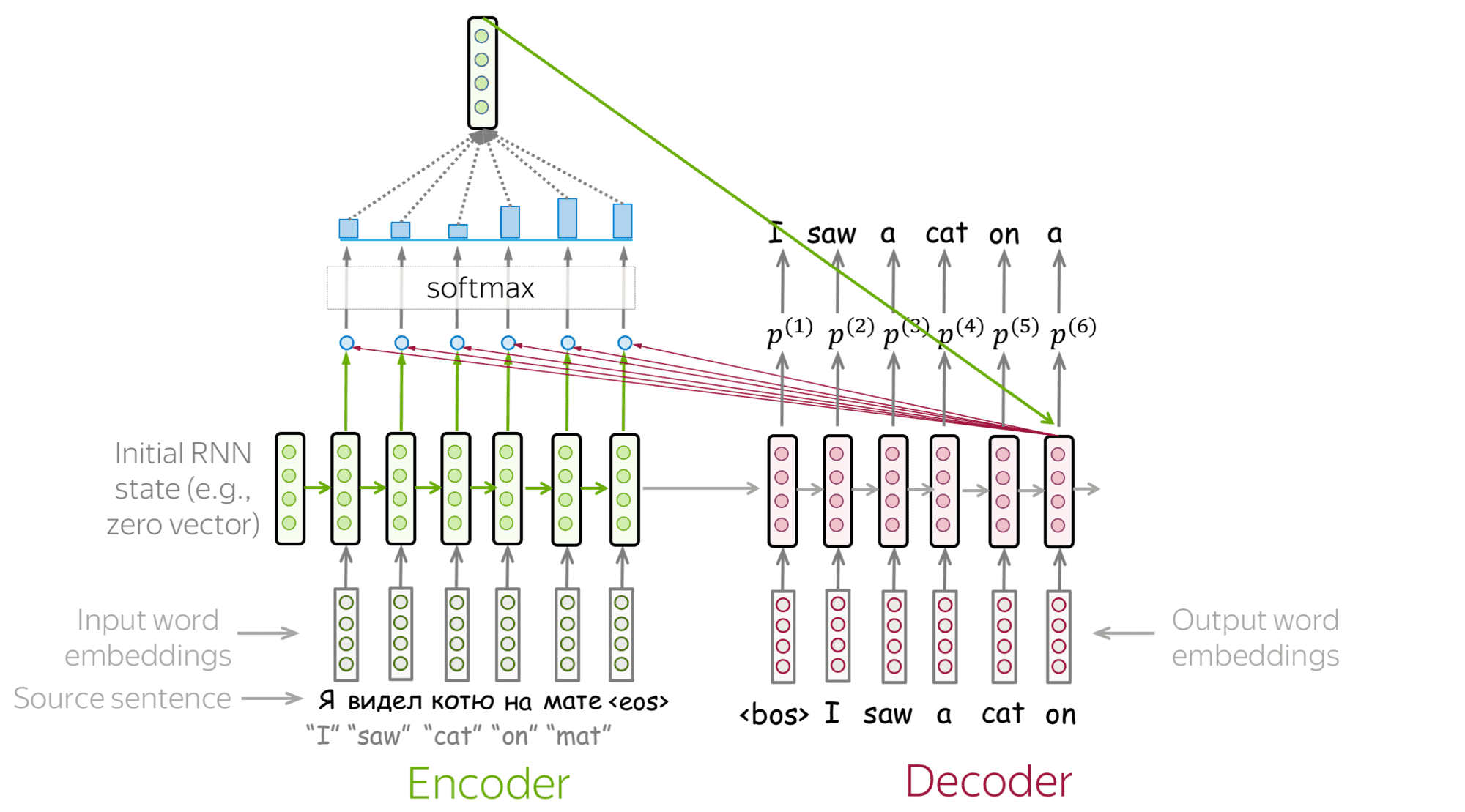
简而言之,attention 就是在 RNN 原来的架构外,给每一个 decoder cell 额外生成了一个 context vector 作为输入。
也就是说 decoder cell 在生成 output 时会综合三个信息来源:input(当前词)、hidden state(前几个词) 和 context vector(全文相关信息)。
这个 context vector 就是 attention 的核心,它通过为所有的 input 计算相关权重,然后摘取重要信息(注意力所在)为当前 output 生成量身定做的 context vector,使得 decoder cell 具有了能够纵览全文且选择性专注于任何重点片段的能力。大幅提高了 RNN 处理长文的能力。
Attention Is All You Need¶
2017 年 6 月 26 日,Google 的研究人员提交了论文《Attention Is All You Need》,提出了名为 transformer 的神经网络结构。
Google 发现,其实根本不需要 RNN,纯粹只靠 attention 就足够了,一系列 attention heads 的组合就可以产生非常好的输出,这就是 transformer,也是那篇著名论文名字的来源。
Attention 的具体构建方式为: (这个 pipeline 的每一个组成部分,都是纯粹的神经网络,没有任何的预先设计)
- 将输入的文字转换为 token
- 将 token 值用神经网络转换为 embedding
- 将每一个 token 在输入中的所在位置,也进行一轮 embedding
- 将两轮 embedding 的结果相加,交给 softmax 函数输出概率向量
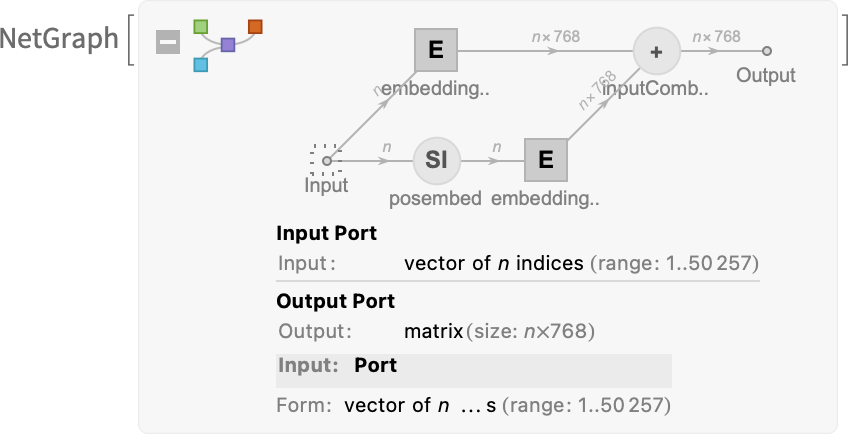
为什么要对 token-value 和 token-position 分别 embedding,然后再相加?
没人知道。
2017 年的某一天 Google 的某个人这么做了,然后发现效果很好…
hello hello hello hello hello hello hello hello hello hello bye bye bye bye bye bye bye bye bye bye 的 attention 块。
可以看到左边的 token-value 块还可以看出明显的重复结构。
最右边就是得到的 attention blocks。 GPT-2 会构建 12 个这样的 attention blocks,ChatGPT 有 96 个。

这一系列 attention heads,扮演的角色,就是为模型推理提供回溯的功能。
前文探讨时 n-grams,这个 N 其实就是提供了直接相连的前 N 个单词的关联。 但是仅仅依靠前面几个词来构建语言上下文显然是不够的。
transfomer 的 attention 机制,就是提供了一种基于语义的回溯能力。
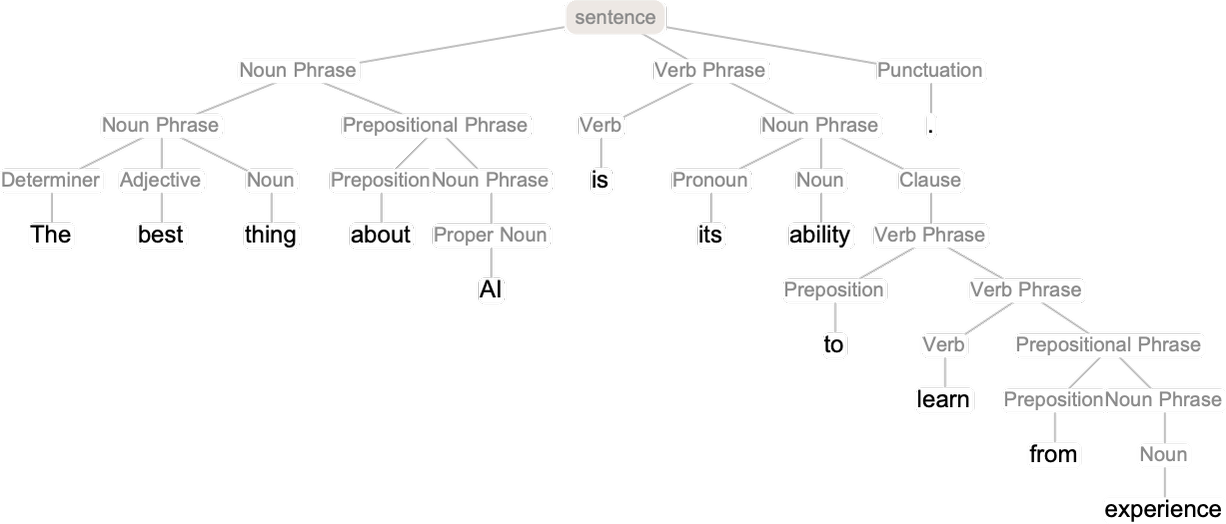
比如当读到句子里的动词时,可以回溯找到主语。 当读到 it 的时候,可以回溯找到代称的名词。这种回溯的距离比 n-gram 更远也更灵活。
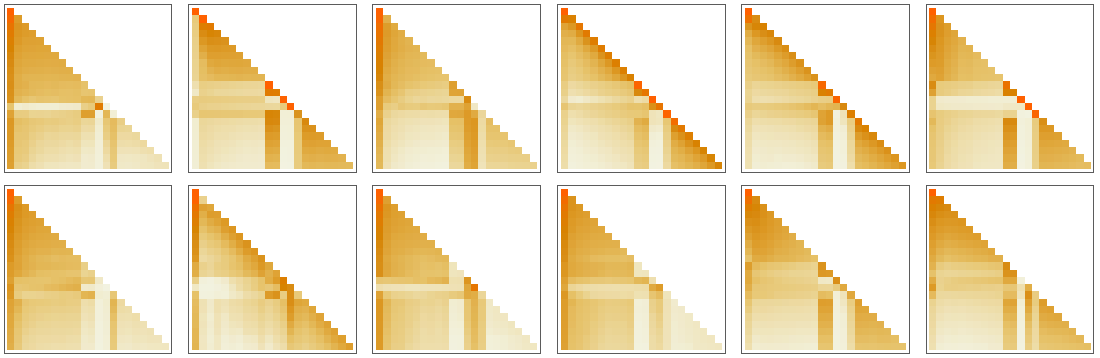
下面这个热力图就是在 12 个 attention heads 的眼中,tokens 间的互相关联程度。横轴和纵轴都是每一个 tokens 的枚举,颜色越深代表关联度越大,越应该被 attention。
这种 attention 机制使得每一个 token 都可以和 input 中的任何一组 tokens 产生关联。而不再是 n-grams 那种死板的静态临近关系。
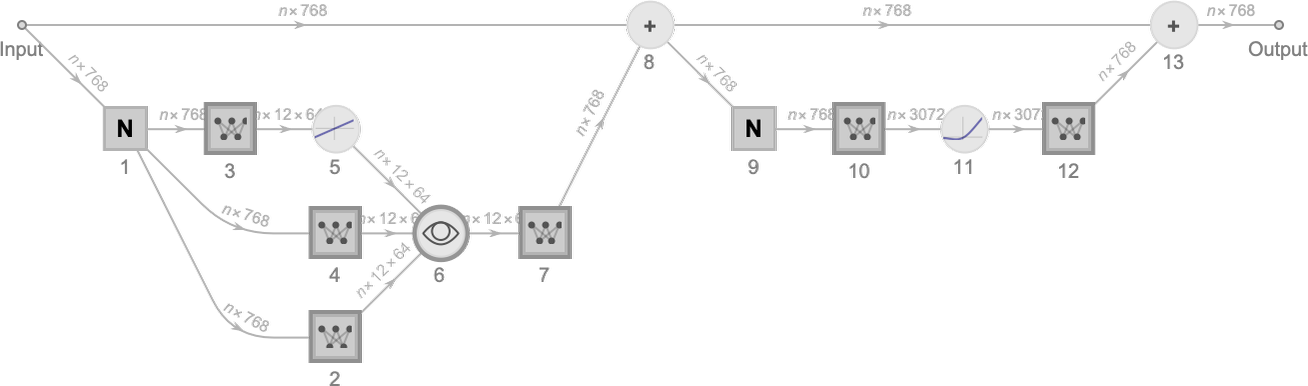
attention heads 会将输入的 tokens vector re-weighted 为一个 embedding vector,然后输入一个巨大的全连接神经网络(GPT-2 位 768 维,GPT-3 位 12288 维)。
很难理解这个网络在干什么,但是我们可以猜想它通过 attention blocks 综合了所有相关的上下文信息。
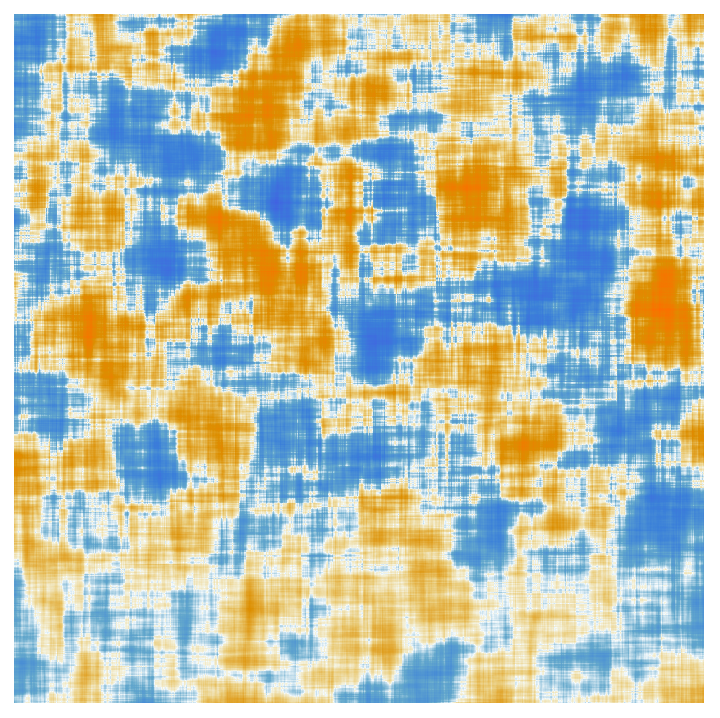
利用投影和滑动平均,我们可以在更低的维度上对其进行可视化。
你可以把这当着神经网络的脑电波图,无论你从中看出了什么…
Turing Machine¶
抛开这些复杂的 pipeline、attention 不谈,整个 GPT 本质上仍然只是一个朴素的神经网络。
最终输出层还是一个 softmax,输出所有 tokens 的概率向量。
这依然只是一个朴素的前馈神经网络,没有 loop,所有的信号按照固定的方向传递,每一次推理的计算复杂度都完全恒定。
所以,这仍然不是一台图灵机,不具备任何复杂计算能力。
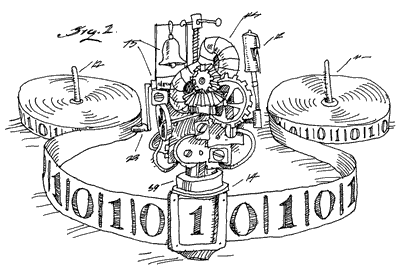
简单回顾一下图灵机。
图灵机的组成非常简单,首先,是一根无限长的纸带,扮演持久化存储。
然后就是一个 CPU,这个 CPU 可以在纸带上前后移动,读取纸带,执行逻辑,然后覆写新的数字或符号。
 |
 |
神经网络和图灵机存在根本的不同:
- 没有持久化存储
- 没有回退
- 没有循环
这导致神经网络缺乏复杂的计算能力,只能做“直觉式”的推理。
(不过我觉得,虽然神经网络存在明显的计算局限性,但是通过不断地抽象迭代 meta neural nets,用高层网络调度底层网络,仍然可以组合出非常复杂的计算逻辑,甚至能实现循环计算。)
GPT 大概有 400 层网络,共计 175B 个连接,也就是 175B 个权重参数。每一次推理,都会让一系列简单数字计算 175B 次。
这也是为什么 GPT 是按照输入输出的长度进行收费的,因为每一个 token 的计算复杂度是恒等的。
拿人脑做个对比,会不会觉得有些奇怪?因为我们回答一个问题所耗费的精力和时间显然和回答的长度无关。这也是人脑,或者自然和神经网络间的本质区别所在。
但是,单个神经网络虽然不是图灵机,由 meta 神经网络调度的神经网络,是图灵机吗?
The Training of ChatGPT¶
GPT 使用了千亿规模的语料词组完成了训练,其神经网络由 1750 亿个参数。
令人吃惊的“巧合”,GPT 的训练集数量和参数数量在同一个量级上。
但是你不能简单地认为 GPT 是把所有的数据集直接存储到网络中了,毕竟网络中只有上千亿个数字。
语言的背后是否存在一些可以简化的内在逻辑?
目前看来 GPT 对信息的压缩能力并不显著,差不多一个权重对应着语料库中的一个 word。
假设神经节点的数量为 N,每一次推理的计算复杂度为 N,训练的计算复杂度为 N^2。这也是为什么 GPT 的训练成本是如此高昂。
- 首先,人类对 LLM 的输出进行打分。
- 然后训练另一个神经网络,能够模拟人类对结果进行打分。
- 最后,将这个新的打分模型作为 cost function 的一部分,应用到原网络。
有趣的是,仅通过原始语料训练出的神经网络就具备足够好的推理能力。并不需要太多人工修订。
GPT 甚至不需要重训练,而是基于 ICL(in-context learning)就可以很好的学会用户 prompt 的指令,并输出内容。
ICL 的神奇能力使 Wolfram 认为,GPT 内蕴含了人类语言和思维的某种本质。 毕竟这个网络真的可以“理解”你的问题。
你不能简单地认为 ICL 是因为问题已经存在于语料库中。 这更像是一种在语料库里识别出 context schema 的思维过程。
而且和人类一样,如果你告诉他的东西完全脱离于它的知识体系, 它就会表现地非常差劲,不知道如何整合自己的知识。
值得在此强调,谨记 LLM 存在算法极限,它学习的是语料的模式, 如果你的问题匹配到了模式,它就可以按照神经网络中的某条路径迅速推理。
LLM 不是图灵机,没有回退和循环,只有网络中的路径推理。所以它不能进行任何实际的运算,无法解答任何 irreducible computation 的问题(除非答案刚好在语料库里!)
What Really Lets ChatGPT Work?¶
人类语言以及生成它所涉及的思维过程,一直被认为是复杂性的顶峰。
而 GPT 破除了这个“迷信”,如今我们知道一个同等复杂度的神经网络,就可以非常出色的生成人类语言。
计算过程可以显著提高系统的复杂性,即使背后的原理非常简单。
我们一直被人类语言的复杂性所蒙蔽了,其实其背后的原理可能就如神经网络一样简单。
神经网络的推理复杂性只需要简单的加法和乘法,就可以表现出非常复杂的行为。
语言就是一个虚假复杂度的例子。它看上去无穷复杂,但是背后的数学原理很简单。 而 LLM 成功地捕捉到了这个背后的基础原理。
GPT 的成功暗示着语言甚至思维的背后存在一个简单的原理。如果理解这个原理,也就能理解 GPT 的工作原理。
但是我们设计一个简化的语言,这个语言由括号构成,语法就是一定要闭合所有的括号。
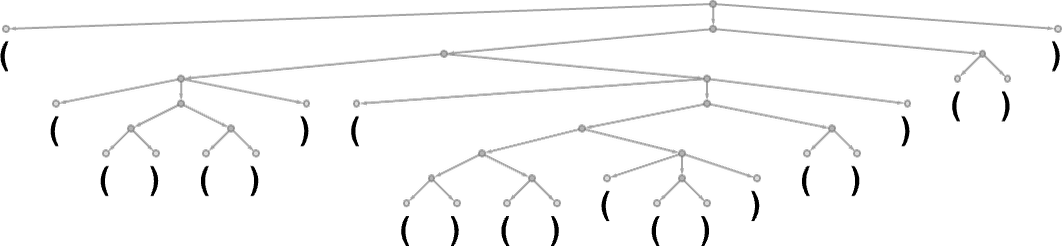
GPT 看上去非常难以学会这门语言。 在经历 40 万次训练后,它仍然难以正确地闭合所有的括号。
左边表现得很好,AI 认为几乎肯定不能在这里结束。
右边就让人有些吃惊了,竟然有 15% 的概率认为这里可以放置一个错误的右括号。
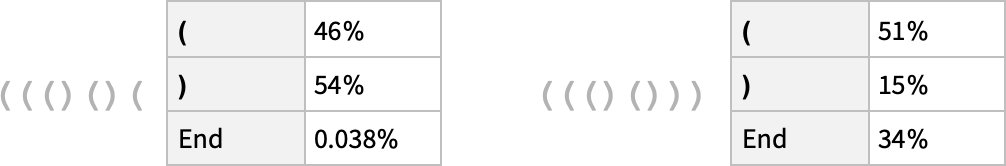
这个现象很令人深思。 神经网络可以学会复杂的人类语言,却无法完成如此简单的数括号任务。
目前人类尚没有一个数理理论来验证一个句子是否有意义,而 GPT 很可能发现了这一理论,使它能够写出有意义的文章。
目前能想到的这个理论最可能的形式,就是逻辑。如亚里士多德的三段论(All X are Y. This is not Y, so it’s not an X),人们正是用逻辑来判断一段话是否有意义,而 GPT 很可能掌握了简单逻辑。
但是在面临更复杂的形式逻辑时,可以预想它的表现不会太好。
我们可以认为神经网络模拟了人类思维中的快思维模式,利于进行快速的直觉响应。但是难以进行复杂严肃的思考,而且非常容易受到锚定效应等影响。

Meaning Space and Semantic Laws of Motion¶
在 meaning space 中追踪 GPT 的推理过程
前文探讨过,每一段文字都会被拆分为一个 tokens 列表,每一个 token 都会被转换为一个 embedding vector,这个 vector 可以视为 GPT meaning space 的坐标。
所以我们可以在这个 meaning space 内把所有的 token 都画出来, 然后 GPT 的推理过程就成为了这个空间的一段连续路径。
通过 embedding,可以将所有的词映射到 meaning space 里

将这个空间投影到二维平面,我们就可以追踪 GPT 的推理过程。 (看不出任何规律😂)
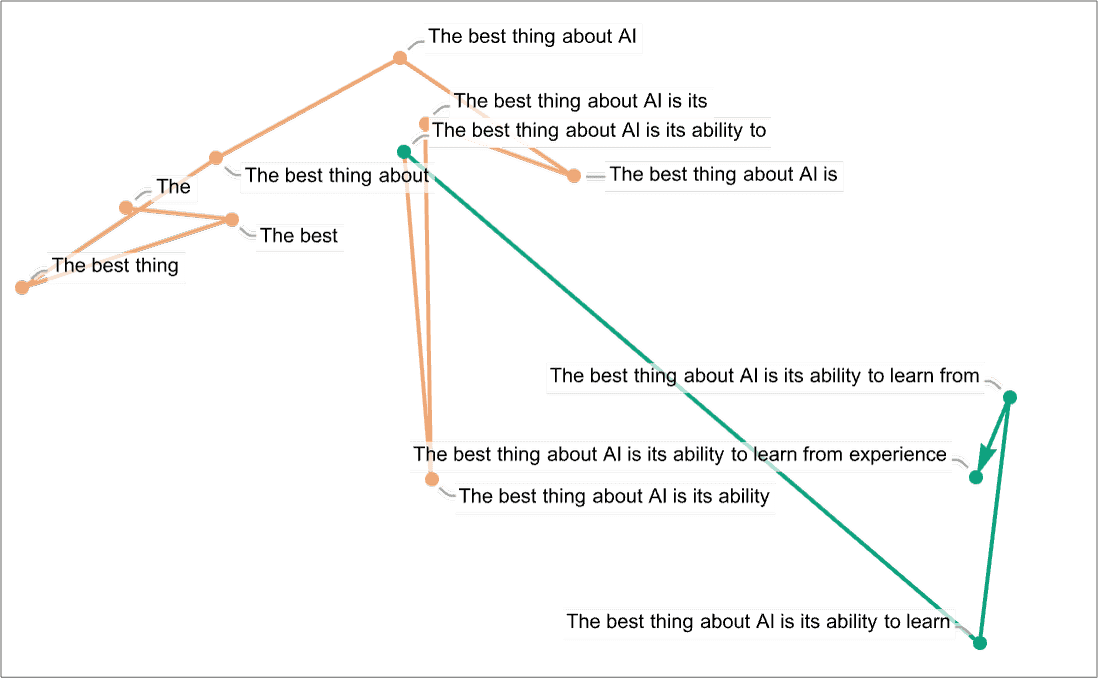
我们可以画出预测下一个词时,一些大概率可选词的方向
(看着像是个扇形,也许预示着下一步推理的大致前进方向)
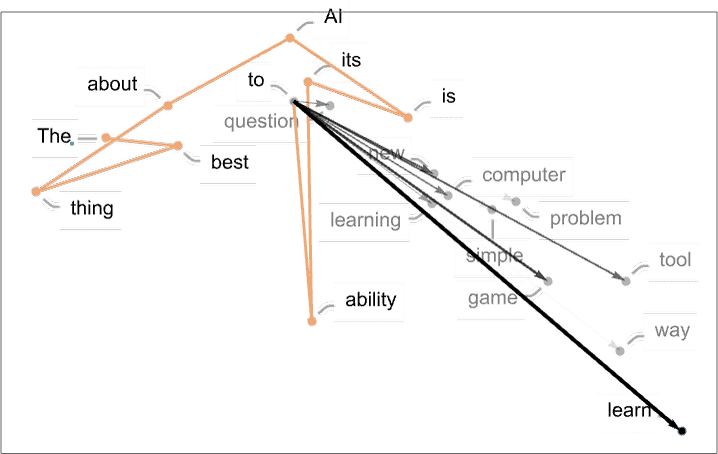
将每一次推理的预测词向量都拼接起来,可以看到每一步的扇形
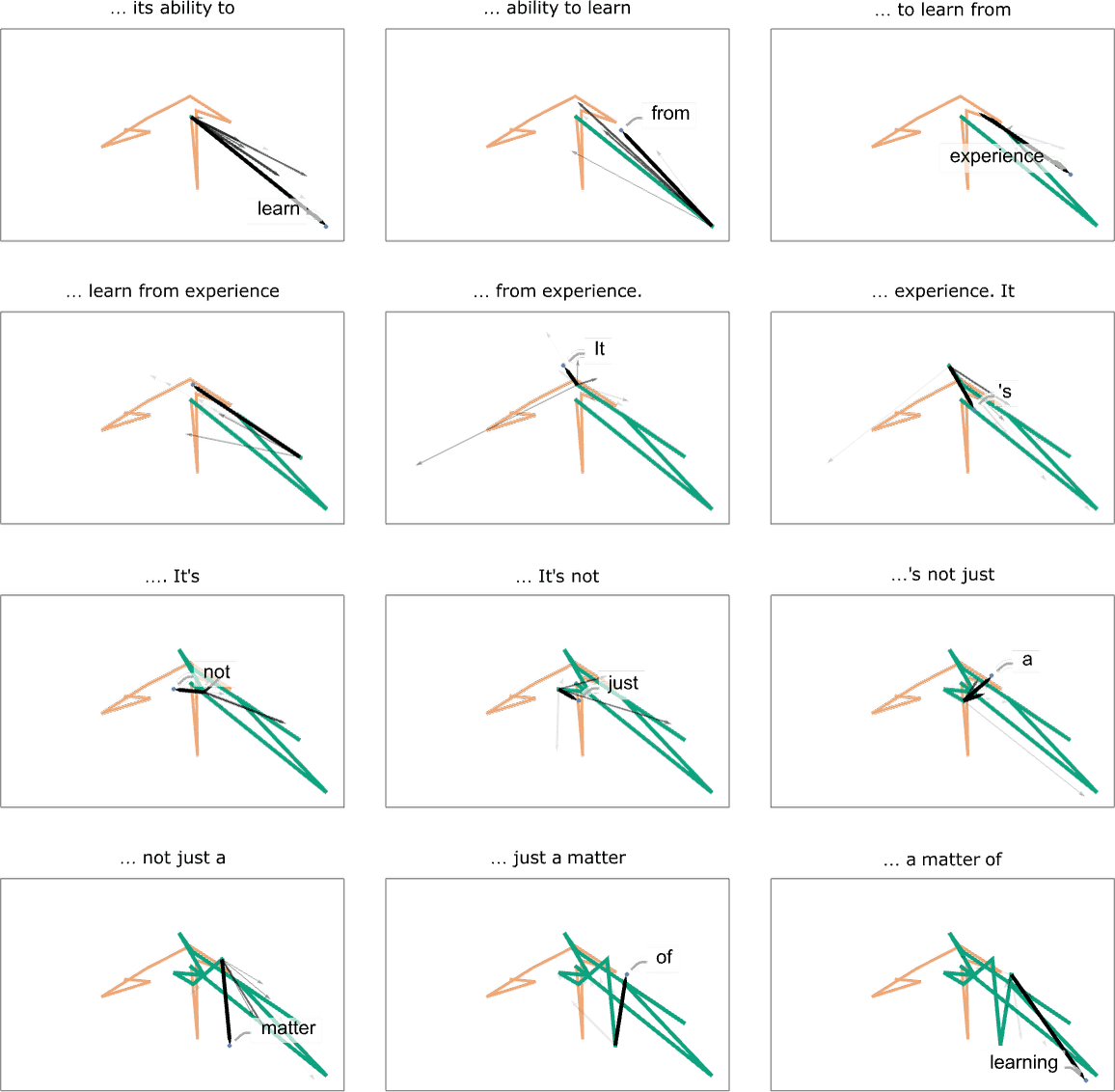
我们还可以在 3D 投影中,追踪 40 步的推理概率图

就目前为止,几乎看不出推理的任何可解释的行为。
但是这是一种尝试解释的思路,我们可以不断地调整投影方式,也许能探索出一条存在某种可理解模式的踪迹。
Semantic Grammar and the Power of Computational Language¶
这一章是对 Wolfram 计算语言的鼓吹。
人类语言天然是不精确的,也没有客观标准,其意义取决于社会共识。
作者认为 GPT 的成功给了他信心,可以构筑出一个形式语义系统, 而且和 GPT 的黑盒神经网络不同,这是可解释的。
GPT 搭配计算语言,可以更轻松地使用各类 irreducible computations 的计算工具。